The Architecture of Life
A universal set of building rules seems to guide the design of organic structures--from simple carbon compounds to complex cells and tissues
SUBTOPICS:
What Is Tensegrity?
How Mechanics Controls Biochemistry
Implications
for Evolution and Beyond
ILLUSTRATIONS: Tensegrity
Transformation (Quicktime)
Cytoskeleton
Architecture
Although researchers have recognized this intriguing fact for some time, most discount it in their quest to explain life's fundamentals. For the past several decades, biologists have attempted to advance our understanding of how the human body works by defining the properties of life's critical materials and molecules, such as DNA, the stuff of genes. Indeed, biologists are now striving to identify every gene in the complete set, known as the genome, that every human being carries. Because genes are the "blueprints" for the key molecules of life, such as proteins, this Holy Grail of molecular biology will lead in the near future to a catalogue of essentially all the molecules from which a human is created. Understanding what the parts of a complex machine are made of, however, does little to explain how the whole system works, regardless of whether the complex system is a combustion engine or a cell. In other words, identifying and describing the molecular puzzle pieces will do little if we do not understand the rules for their assembly.
That nature applies common assembly rules is implied by the recurrence--at scales from the molecular to the macroscopic--of certain patterns, such as spirals, pentagons and triangulated forms. These patterns appear in structures ranging from highly regular crystals to relatively irregular proteins and in organisms as diverse as viruses, plankton and humans. After all, both organic and inorganic matter are made of the same building blocks: atoms of carbon, hydrogen, oxygen, nitrogen and phosphorus. The only difference is how the atoms are arranged in three-dimensional space.
This phenomenon, in which components join together to form larger, stable structures having new properties that could not have been predicted from the characteristics of their individual parts, is known as self-assembly. It is observed at many scales in nature. In the human body, for example, large molecules self-assemble into cellular components known as organelles, which self-assemble into cells, which self-assemble into tissues, which self-assemble into organs. The result is a body organized hierarchically as tiers of systems within systems. Thus, if we are to understand fully the way living creatures form and function, we need to uncover these basic principles that guide biological organization.
Despite centuries of study, researchers still know relatively little about the forces that guide atoms to self-assemble into molecules. They know even less about how groups of molecules join together to create living cells and tissues. Over the past two decades, however, I have discovered and explored an intriguing and seemingly fundamental aspect of self-assembly. An astoundingly wide variety of natural systems, including carbon atoms, water molecules, proteins, viruses, cells, tissues and even humans and other living creatures, are constructed using a common form of architecture known as tensegrity. The term refers to a system that stabilizes itself mechanically because of the way in which tensional and compressive forces are distributed and balanced within the structure.
This fundamental finding could one day have practical applications in many areas. For example, new understanding of tensegrity at the cellular level has allowed us to comprehend better how cellular shape and mechanical forces--such as pressure in blood vessels or compression in bone--influence the activities of genes. At the same time, deeper understanding of natural rules of self-assembly will allow us to make better use--in applications ranging from drug design to tissue engineering--of the rapidly accumulating data we have about molecules, cells and other biological components. An explanation of why tensegrity is so ubiquitous in nature may also provide new insight into the very forces that drive biological organization--and perhaps into evolution itself.
My interest in tensegrity dates back to my undergraduate years in the mid-1970s at Yale University. There my studies of cell biology and also of sculpture led me to realize that the question of how living things form has less to do with chemical composition than with architecture. The molecules and cells that form our tissues are continually removed and replaced; it is the maintenance of pattern and architecture, I reasoned, that we call life.
Tensegrity structures are mechanically stable not because of the strength of individual members but because of the way the entire structure distributes and balances mechanical stresses. The structures fall into two categories. Structures in one category, which includes the geodesic domes of Buckminster Fuller, are basically frameworks made up of rigid struts, each of which can bear tension or compression. The struts that make up the framework are connected into triangles, pentagons or hexagons, and each strut is oriented so as to constrain each joint to a fixed position, thereby assuring the stability of the whole structure.
The other category of tensegrity structures encompasses those that stabilize themselves through a phenomenon known as prestress. This type of structure was first constructed by the sculptor Kenneth Snelson. In Snelson's elegant sculptures, structural members that can bear only tension are distinct from those that bear compression. Even before one of these structures is subjected to an external force, all the structural members are already in tension or compression--that is, they are prestressed. Within the structure, the compression-bearing rigid struts stretch, or tense, the flexible, tension-bearing members, while those tension-bearing members compress the rigid struts. These counteracting forces, which equilibrate throughout the structure, are what enable it to stabilize itself.
Tensegrity structures of both categories share one critical feature, which is that tension is continuously transmitted across all structural members. In other words, an increase in tension in one of the members results in increased tension in members throughout the structure--even ones on the opposite side. This global increase in tension is balanced by an increase in compression within certain members spaced throughout the structure. In this way, the structure stabilizes itself through a mechanism that Fuller described as continuous tension and local compression. In contrast, most buildings derive their stability from continuous compression because of the force of gravity.
The tension-bearing members in these structures--whether Fuller's domes or Snelson's sculptures--map out the shortest paths between adjacent members (and are therefore, by definition, arranged geodesically). Tensional forces naturally transmit themselves over the shortest distance between two points, so the members of a tensegrity structure are precisely positioned to best withstand stress. For this reason, tensegrity structures offer a maximum amount of strength for a given amount of building material.
What does tensegrity have to do with the human body? The principles of tensegrity apply at essentially every detectable size scale in the body. At the macroscopic level, the 206 bones that constitute our skeleton are pulled up against the force of gravity and stabilized in a vertical form by the pull of tensile muscles, tendons and ligaments (similar to the cables in Snelson's sculptures). In other words, in the complex tensegrity structure inside every one of us, bones are the compression struts, and muscles, tendons and ligaments are the tension-bearing members. At the other end of the scale, proteins and other key molecules in the body also stabilize themselves through the principles of tensegrity. My own interest lies in between these two extremes, at the cellular level.
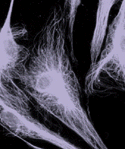
As a graduate student working with James D. Jamieson at Yale, I focused on how the components of biological systems--especially of cells--interacted mechanically. At this time, in the late 1970s, biologists generally viewed the cell as a viscous fluid or gel surrounded by a membrane, much like a balloon filled with molasses. Cells were known to contain an internal framework, or cytoskeleton, composed of three different types of molecular protein polymers, known as microfilaments, intermediate filaments and microtubules. But their role in controlling cell shape was poorly understood.
Another mystery in those days concerned the way isolated cells behave when placed on different surfaces. It had been long known that cells spread out and flatten when they attach to a rigid glass or plastic culture dish. In 1980, however, Albert K. Harris of the University of North Carolina at Chapel Hill showed that when affixed to a flexible rubber substrate, cells contract and become more spherical. This contraction bunches up, or puckers, the underlying rubber.
It occurred to me that a view of the cell as a tensegrity structure could easily explain such behavior. I modeled a cell as such a structure; it consisted of six wood dowels and some elastic string. I arranged the dowels--which bore the compressive stress--in three pairs. Each pair was perpendicular to the other two, and none of the wood struts actually touched one another. A tension-bearing elastic string connected to the ends of all the dowels, pulling them into a stable, three-dimensional form. I also placed a smaller, spherical tensegrity model, representing the nucleus, within the larger one that represented the rest of the cell. Then, to mimic cytoskeletal connections between the nucleus and the rest of the cell, I stretched elastic strings from the surface of the large tensegrity structure to the smaller one inside.
To understand how my experiment worked, it is necessary to know that pushing down on a tensegrity model of the kind I built forces it into what appears to be a flattened pile of sticks and string. As soon as the pressure is removed, the energy stored in the tensed filaments causes the model to spring back to its original, roughly spherical shape. To simulate how cells behave when placed on a surface, I mimicked a solid culture substrate of glass or plastic by stretching a piece of cloth taut and pinning it firmly to a piece of wood below. I affixed the tensegrity model to the substrate by flattening it and sewing the ends of some of the dowels to the cloth. These attachments were analogous to the cell-surface molecules, now known as integrins or adhesion receptors, that physically connect a cell to its anchoring substrate.
With the dowel ends sewed to the tightly pinned cloth, the model remained flat, just as a real cell does on a hard substrate. When I lifted the pins to free the cloth from the wood, however, thereby making the cell's anchoring surface flexible, the tensegrity model popped up into its more spherical form, puckering the cloth underneath. Furthermore, I noticed that when I stretched the model flat by connecting it to the cloth substrate, the cell and nucleus inside it extended in a coordinated manner. The nucleus model also moved toward the bottom of the simulated cell. Soon thereafter, I showed experimentally that living cells and nuclei spread and polarize in a similar manner when they adhere to a substrate. Thus, with my highly simplified construction, I showed that tensegrity structures mimic the known behavior of living cells.
In the years since my modeling experiment, biologists have learned a great deal about the mechanical aspects of cells, and their findings seem to confirm that cells do indeed get their shape from tensegrity. Further, just as the models predict, most cells derive their structure not only from the cytoskeleton's three major types of filaments but also from the extracellular matrix--the anchoring scaffolding to which cells are naturally secured in the body.
|
If the cell and nucleus are physically connected by tensile filaments and not solely by a fluid cytoplasm, then pulling on receptors at the cell surface should produce immediate structural changes deep inside the cell. Recently Andrew Maniotis, who was in my group at Children's Hospital of Harvard Medical School, demonstrated this directly. By binding micropipettes to adhesion receptors on the surface of living cells and pulling outward, Maniotis caused cytoskeletal filaments and structures in the nucleus to realign immediately in the direction of pull. Thus, as my early experiments suggested, cells and nuclei do not behave like viscous water balloons.
How Mechanics Controls Biochemistry
Tensegrity can be invoked to explain more than the stabilization of cellular and nuclear form. For example, Steven R. Heidemann, working with Harish Joshi and Robert E. Buxbaum of Michigan State University in the mid-1980s, found that tensegrity can explain how nerve cells extend long, thin projections called neurites, which are filled with microtubules and transmit electrical signals in the nervous system. This growth is required for repair of nerve damage.
Heidemann's group found that microtubules are compressed at their ends by the pull of surrounding contractile microfilaments inside the neurites. More important, the researchers discovered that microtubule assembly (elongation)--and, hence, neurite extension--is promoted by shifting compressive loads off the microtubule and onto the cell's attachments to its extracellular matrix. In other words, the existence of a tensegrity force balance provides a means to integrate mechanics and biochemistry at the molecular level.
Very recently, Andrew Matus of the Friedrich Miescher Institute in Basel added a vivid footnote to this story. By making cells that produce fluorescent microtubules, Matus actually viewed those microtubules buckling under compression.
The tensegrity model suggests that the structure of the cell's cytoskeleton can be changed by altering the balance of physical forces transmitted across the cell surface. This finding is important because many of the enzymes and other substances that control protein synthesis, energy conversion and growth in the cell are physically immobilized on the cytoskeleton. For this reason, changing cytoskeletal geometry and mechanics could affect biochemical reactions and even alter the genes that are activated and thus the proteins that are made.
To investigate this possibility further, Rahul Singhvi and Christopher S. Chen in my group, working with George M. Whitesides, also at Harvard, developed a method to engineer cell shape and function. They forced living cells to take on different shapes--spherical or flattened, round or square--by placing them on tiny, adhesive "islands" composed of extracellular matrix. Each adhesive island was surrounded by a Teflon-like surface to which cells could not adhere.
By simply modifying the shape of the cell, they could switch cells between different genetic programs. Cells that spread flat became more likely to divide, whereas round cells that were prevented from spreading activated a death program known as apoptosis. When cells were neither too extended nor too retracted, they neither divided nor died. Instead they differentiated themselves in a tissue-specific manner: capillary cells formed hollow capillary tubes; liver cells secreted proteins that the liver normally supplies to the blood; and so on.
Thus, mechanical restructuring of the cell and cytoskeleton apparently tells the cell what to do. Very flat cells, with their cytoskeletons stretched, sense that more cells are needed to cover the surrounding substrate--as in wound repair--and that cell division is needed. Rounding indicates that too many cells are competing for space on the matrix and that cells are proliferating too much; some must die to prevent tumor formation. In between these two extremes, normal tissue function is established and maintained. Understanding how this switching occurs could lead to new approaches to cancer therapy and tissue repair and perhaps even to the creation of artificial-tissue replacements.
The next level up in the hierarchy of self-assembly is the formation of tissues, which are created from the joining of cells to one another and to their extracellular matrix. One emergent property of tissues is how they behave mechanically. Many different types of tissue, including muscle, cartilage, blood vessels and skin, exhibit a response known as linear stiffening. If you pull on your skin, for example, you will feel the resistance increase as you tug harder. An increasing external force is met with increasing resistance. Recent studies show that even isolated molecules, such as DNA, exhibit linear stiffening, yet until we examined this phenomenon in the context of tensegrity, there was no mechanical or mathematical explanation for this behavior.
In 1993 my co-worker Ning Wang, working with James P. Butler of the Harvard School of Public Health, developed a device that allowed us to twist individual molecules on the surface membrane of living cells while simultaneously measuring the cellular response. We found that when we increased the stress applied to integrins (molecules that go through the cell's membrane and link the extracellular matrix to the internal cytoskeleton), the cells responded by becoming stiffer and stiffer--just as whole tissues do. Furthermore, living cells could be made stiff or flexible by varying the prestress in the cytoskeleton by changing, for example, the tension in contractile microfilaments.

|
Although the exact details of the interaction are not all known, we showed, using a stick-and-string tensegrity model, that the gist of the response can be discerned from the way in which tensegrity structures respond to stress. Essentially, all the interconnected structural elements of a tensegrity model rearrange themselves in response to a local stress. Linear stiffening results because as the applied stress increases, more of the members come to lie in the direction of the applied stress.
Working with Dimitrije Stamenovic of Boston University, we developed a mathematical model based on these principles. It predicts, for the first time, the linear-stiffening response of tissues, living cells and even molecules. We hope to use this model to help design advanced materials that have the linear-stiffening property and that may be useful in such applications as protective clothing and artificial body parts. The same mathematical approach may also be incorporated within computer programs as a shortcut to accelerate molecular modeling and drug design.
In Wang's magnetic-twisting studies and in Maniotis's micropipette-pulling experiments, we found that applying stress to cell-surface receptors involved with metabolism--rather than adhesion--did not effectively convey force to the inside of the cell. Thus, these studies confirmed that mechanical forces are transmitted over specific molecular paths in living cells, a finding that provided new insight into how cells sense mechanical stimuli that regulate tissue development. This insight, in turn, may help us better understand a wide variety of phenomena, from the growth of muscle in response to tension to the growth of plant roots in response to gravity.
Although the tensegrity models predicted many cell behaviors, one disparity needed explaining. Many cells can spread and flatten without microtubules--the most important compression struts in the model. If living cells can change from spherical to flat without these struts, how can tensegrity apply? Again using an uncomplicated modeling approach, I found that, incredibly, the microfilament network itself is a tensegrity structure.
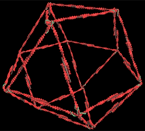
In the cytoskeleton of a living cell, contractile microfilaments form a lattice that reorganizes locally into different forms, such as large bundles or networks of triangles. To explore the mechanism behind this reorganization, I modeled the microfilament lattice as a polyhedral framework of soda straws that contained six triangles and four squares. The straws were held together by a single elastic string that I threaded through all the straws and tied to itself. I assumed that each soda straw in the model represented a single contractile microfilament that could generate mechanical tension by shortening itself. It is known that contractile microfilaments get stiffer when they shorten. Thus, the internal elastic thread in the model would then mimic the continuous tension in the whole structure that results from the shortening of all these stiffened filaments.
|
I assumed that this soda-straw model represented one modular cytoskeletal unit that interconnected in all directions with other similar modules in a round, unattached (suspended) cell. The question I was trying to answer was, What would happen to this framework if the cell it supported were to attach to a rigid surface?
Cells attach by binding to surface-bound molecules in the extracellular matrix. But cells are not evenly "glued" to the matrix; rather they are "spot welded" in localized sites known as focal adhesions. Contractile microfilaments respond to anchorage by shortening and increasing isometric tension within the lattice. The soda-straw models suggested that the increasing tension produced by attachment would cause the individual contractile microfilaments that formed the squares in the model to self-assemble into linear bundles stretching between these focal-adhesion sites where integrin receptors anchor the cell to the matrix. In fact, when living cells spread on a surface, individual contractile microfilaments align in a nearly identical manner to form bundles called stress fibers.
In contrast, at the top of the cell, there is no adhesive substrate to resist the pull of the shortening microfilaments. In these regions the contraction of each microfilament can be resisted only by the pull and stiffness of its neighboring filaments. Fuller showed many years ago that inward pulling and twisting causes this type of polyhedral structure to undergo what he called a jitterbug-transformation: the highly flexible framework of squares and triangles converts into fully triangulated octahedral or tetrahedral forms--or, in other words, into fully triangulated tensegrity structures.
When I interconnected many similar soda-straw models, I found that the individual modules progressively contracted, resulting in the formation of a geodesic framework composed of alternating octahedral and tetrahedral forms, closely packed. In a cell, contraction of surrounding microfilament networks that interconnect with the cell base would bend this framework down over the spherical nucleus, thereby transforming it into a highly triangulated dome--specifically, a geodesic dome.
Elias Lazarides, then at Cold Spring Harbor Laboratory in New York, and Mary Osborn and Klaus Weber of the Max Planck Institute in Göttingen, Germany, observed these very transformations in the region of the cytoplasm above the nucleus in spreading cells. Significantly, the existence of a geodesic dome within the cytoskeleton at the molecular level demonstrates conclusively that cells can and do use the architecture of tensegrity to shape their cytoskeleton.
The geodesic structure found within the cytoskeleton is a classic example of a pattern that is found everywhere in nature, at many different size scales. Spherical groups of carbon atoms called buckminsterfullerenes or buckyballs, along with viruses, enzymes, organelles, cells and even small organisms, all exhibit geodesic forms. Strangely, few researchers seem to have asked why this is so. My view is that this recurrent pattern is visual evidence of the existence of common rules for self-assembly. In particular, all these entities stabilize themselves in three dimensions in a similar way: by arranging their parts to minimize energy and mass through continuous tension and local compression--that is, through tensegrity.
The assembly of viruses, the smallest form of life on the earth, involves binding interactions between many similar proteins that come together to form a geodesic viral coat that encloses the genetic material. During virus formation, linear extensions of the proteins overlap with similar tails that extend from neighboring proteins to form a triangulated geodesic framework on the nanometer scale. Each joint in this framework self-stabilizes as a result of a balance between the pull of intermolecular attractive forces (hydrogen bonds) and the ability of the individual protein tails to resist compression and buckling.
The same basic scheme is apparent in buckyballs, except that the building blocks are atoms instead of proteins. In buckyballs, 60 carbon atoms form a geodesic sphere covered by 20 hexagons interspersed with 12 pentagons: the pattern on a soccer ball. In effect, the 90 carbon-carbon bonds in a buckyball are the struts in a tensegrity sphere.
It is more difficult, however, to see that the same building rules also apply to irregular structures, including many biological molecules, that do not exhibit geodesic forms. Proteins, on which cells depend for structure, catalysis and many other functions, are long strings of amino acids. Small regions of the protein's amino acid backbone fold into helical forms that stabilize themselves through a balance between the attractive force of hydrogen bonds (pulling together different regions of the molecule) and the ability of the protein coil to resist shortening, or compression. In other words, these helical regions stabilize themselves through tensegrity--as does any helical molecule, such as DNA.
Protein organization also involves hierarchical assembly. The small regions of a protein that are helically stiffened are separated from one another by parts of the same amino acid backbone that act as if they were flexible hinges. These strutlike regions fold back on themselves (because of tensile hydrogen-bonding forces) in order to stabilize the entire molecule. The stiffened helices may be extremely compressed locally, even though forces are equilibrated across the whole prestressed molecule.
Because a local force can change the shape of an entire tensegrity structure, the binding of a molecule to a protein can cause the different, stiffened helical regions to rearrange their relative positions throughout the length of the protein. For example, when a signal-bearing molecule binds to a receptor that goes through the membrane and into a cell, the attachment can cause conformational changes at the opposite end of the receptor. These conformational changes, in turn, alter the shape of adjacent proteins and trigger a cascade of molecular restructuring inside that cell. Indeed, this is how cells sense and respond to changes in their environment.
Thus, from the molecules to the bones and muscles and tendons of the human body, tensegrity is clearly nature's preferred building system. Only tensegrity, for example, can explain how every time that you move your arm, your skin stretches, your extracellular matrix extends, your cells distort, and the interconnected molecules that form the internal framework of the cell feel the pull--all without any breakage or discontinuity.
Remarkably, tensegrity may even explain how all these phenomena are so perfectly coordinated in a living creature. At the Johns Hopkins School of Medicine, Donald S. Coffey and Kenneth J. Pienta found that tensegrity structures function as coupled harmonic oscillators. DNA, nuclei, cytoskeletal filaments, membrane ion channels and entire living cells and tissues exhibit characteristic resonant frequencies of vibration. Very simply, transmission of tension through a tensegrity array provides a means to distribute forces to all interconnected elements and, at the same time, to couple, or "tune," the whole system mechanically as one.
Implications for Evolution and Beyond
Although changes in DNA generate biological diversity, genes are a product of evolution, not its driving force. In fact, geodesic forms similar to those found in viruses, enzymes and cells existed in the inorganic world of crystals and minerals long before DNA ever came into existence. Even water molecules are structured geodesically.
The relevant question is, How did organic molecules and cells evolve from inorganic components? After all, in terms of how emergent properties arise, self-assembly of molecules into organelles or cells into tissues is not very different from the self-assembly of atoms into compounds. For example, sodium, an explosive metal, and chlorine, a poisonous gas, combine to form sodium chloride, whose emergent property is that it can be used as table salt. The important principle here is the manner in which a structure shapes itself and holds its subcomponents together in three-dimensional space; this characteristic is what defines the way the structure as a whole will behave.
More broadly, all matter is subject to the same spatial constraints, regardless of scale or position. Thus, given these constraints, tensegrity is the most economical and efficient way to build--at the molecular scale, at the macroscopic scale and at all scales in between. It is possible that fully triangulated tensegrity structures may have been selected through evolution because of their structural efficiency--their high mechanical strength using a minimum of materials. The flexibility exhibited by prestressed tensegrity structures would be advantageous because it allows structures to take on different shapes. For example, if a molecule or cell were able to transform into a shape that was more stable at a certain temperature or pressure, or more efficient metabolically, then its lifetime would have been extended. It would have been more likely to interact with other, similar entities and then to self-assemble once again.
Researchers now think biological evolution began in layers of clay, rather than in the primordial sea. Interestingly, clay is itself a porous network of atoms arranged geodesically within octahedral and tetrahedral forms. But because these octahedra and tetrahedra are not closely packed, they retain the ability to move and slide relative to one another. This flexibility apparently allows clay to catalyze many chemical reactions, including ones that may have produced the first molecular building blocks of organic life.
Over time, different molecular collectives self-assembled to form the first structures with specialized functions--the forerunners of present-day organelles--which then combined with one another to create the first simple cells. These cells then produced proteins that self-assembled to form extracellular matrix--anchoring scaffolds that, in turn, promoted self-assembly of multicellular tissues. Organs developed from the self-assembly of tissues, and complex organisms arose through combination and progressive remodeling of different organs. Indeed, the development of an embryo from a sperm and an egg recapitulates all these stages of self-assembly.
The emergence of DNA and genes gave rise to a new mechanism for generating structural diversity that accelerated evolution. Yet throughout all this time the rules guiding the process of hierarchical self-assembly remained essentially unchanged. So it is no surprise that the basic arrangement of bones and muscles is remarkably similar in Tyrannosaurus rex and Homo sapiens; that animals, insects and plants all rely on prestress for the mechanical stability of their bodies; and that geodesic forms, such as hexagons, pentagons and spirals, predominate in natural systems.
Finally, more philosophical questions arise: Are these building principles universal? Do they apply to structures that are molded by very large scale forces as well as small-scale ones? We do not know. Snelson, however, has proposed an intriguing model of the atom based on tensegrity that takes off where the French physicist Louis de Broglie left off in 1923. Fuller himself went so far as to imagine the solar system as a structure composed of multiple nondeformable rings of planetary motion held together by continuous gravitational tension. Then, too, the fact that our expanding (tensing) universe contains huge filaments of gravitationally linked galaxies and isolated black holes that experience immense compressive forces locally can only lead us to wonder. Perhaps there is a single underlying theme to nature after all. As suggested by early 20th-century Scottish zoologist D'Arcy W. Thompson, who quoted Galileo, who, in turn, cited Plato: the Book of Nature may indeed be written in the characters of geometry.
Further Reading
ON GROWTH AND FORM. REVISED EDITION. D'Arcy W. Thompson. Cambridge University Press, 1942 (reprinted 1992).
MOVEMENT AND SELF-CONTROL IN PROTEIN ASSEMBLIES. Donald L. D. Caspar in Biophysical Journal, Vol. 32, No. 1, pages 103--138; October 1980.
CLAY MINERALS AND THE ORIGIN OF LIFE. Edited by A. Graham Cairns-Smith and Hyman Hartman. Cambridge University Press, 1986.
CELLULAR TENSEGRITY: DEFINING NEW RULES OF BIOLOGICAL DESIGN THAT GOVERN THE CYTOSKELETON. Donald E. Ingber in Journal of Cell Science, Vol. 104, No. 3, pages 613--627; March 1993.
MECHANOTRANSDUCTION ACROSS THE CELL SURFACE AND THROUGH THE CYTOSKELETON. Ning Wang, James P. Butler and Donald E. Ingber in Science, Vol. 260, pages 1124--1127; May 21, 1993.
GEOMETRIC CONTROL OF CELL LIFE AND DEATH. Christopher S. Chen, Milan Mrksich, Sui Huang, George M. Whitesides and Donald E. Ingber in Science, Vol. 276, pages 1425--1428; May 30, 1997.
TENSEGRITY: THE ARCHITECTURAL BASIS OF CELLULAR MECHANOTRANSDUCTION. Donald E. Ingber in Annual Review of Physiology, Vol. 59, pages 575--599; 1997.
Related Links
Biological design principles that guide self-organization, emergence, and hierarchical assembly: from complexity to tensegrity by Donald E. Ingber
Cell Biology: Force-Carrying Web Pervades Living Cell by James Glanz
MIT Center for Biomedical Engineering
The Author
DONALD E. INGBER, who holds B.A., M.A., M.Phil., M.D. and Ph.D. degrees from Yale University, is an associate professor of pathology at Harvard Medical School and a research associate in the departments of surgery and pathology at Children's Hospital in Boston. He is also a member of the Center for Bioengineering at the Massachusetts Institute of Technology. In addition to his work on cell structure, Ingber has contributed to the study of tumor angiogenesis, including the discovery of an anticancer drug now in clinical trials. He is the founder of Molecular Geodesics, Inc., a Cambridge, Mass., company that creates advanced materials with biologically inspired properties.
